
When the definition of continuity is applied to f( x) at x = 0, you find that When the definition of continuity is applied to f( x) at x = 2, you find that When the definition of continuity is applied to f( x) at x = 2, you find that f(2) does not exist hence, f is not continuous (discontinuous) at x = 2. When the definition of continuity is applied to f( x) at x = −4, you find that Note that the greatest integer function is continuous from the right and from the left at any noninteger value of x.Įxample 1: Discuss the continuity of f( x) = 2 x + 3 at x = −4. Hence, and f( x) is not continuous at n from the left. The greatest integer function is continuous at any integer n from the right only because The greatest integer function,, is defined to be the largest integer less than or equal to x (see Figure 1).įigure 1 The graph of the greatest integer function y =. Many of our familiar functions such as linear, quadratic and other polynomial functions, rational functions, and the trigonometric functions are continuous at each point in their domain.Ī special function that is often used to illustrate one‐sided limits is the greatest integer function.
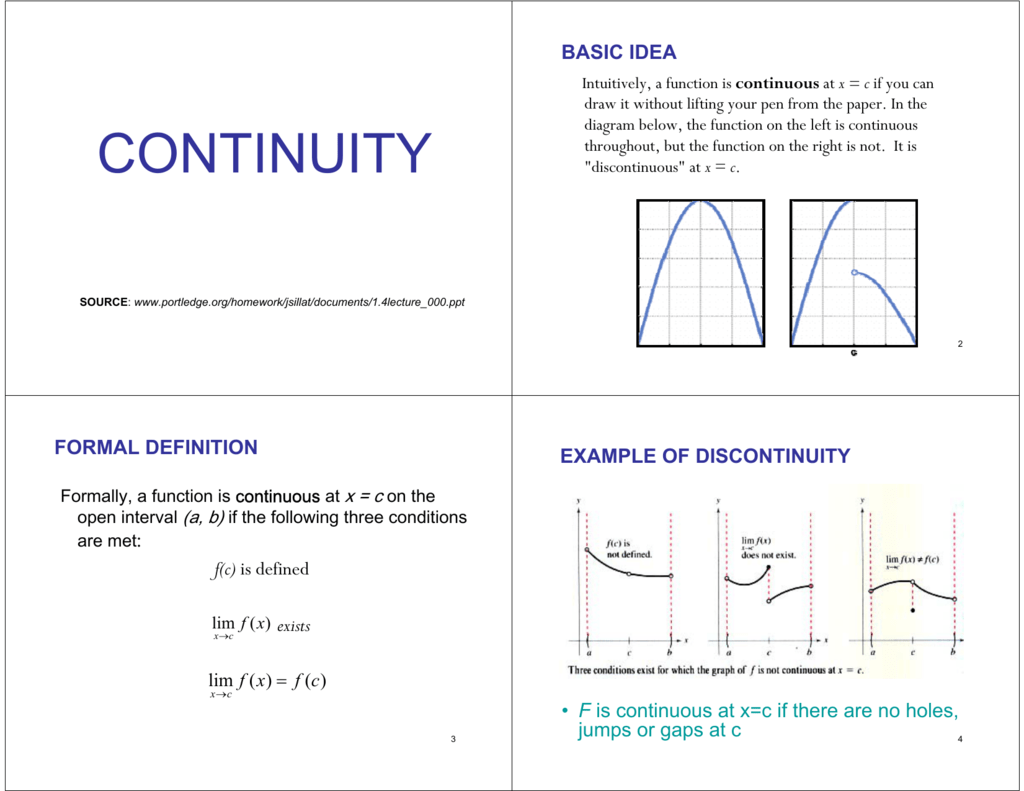
A function is said to be continuous at ( c, f( c)) from the right if and continuous at ( c, f( c)) from the left if. Geometrically, this means that there is no gap, split, or missing point for f( x) at c and that a pencil could be moved along the graph of f( x) through ( c, f( c)) without lifting it off the graph. Volumes of Solids with Known Cross SectionsĪ function f( x) is said to be continuous at a point ( c, f( c)) if each of the following conditions is satisfied:.Second Derivative Test for Local Extrema.First Derivative Test for Local Extrema.Differentiation of Exponential and Logarithmic Functions.Differentiation of Inverse Trigonometric Functions.

Limits Involving Trigonometric Functions.


 0 kommentar(er)
0 kommentar(er)
